Números primos y compuestos. Criterios de divisibilidad

Conceptos básicos

Divisible
Decimos que el número a es divisible entre el número b si b divide a a, es decir, si la división de a entre b tiene resto 0.

También podemos decir divisible por en lugar de divisible entre.

Ejemplos:

• 4 es divisible entre 2:
  
  
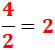
• 15 es divisible por 3 y por 5:
  
  

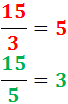
Múltiplo

Decimos que Un número b es un múltiplo de a si hay otro número n(entero) tal que 

b = a · n

NÚMEROS PRIMOS 

Decimos que un número es un número primo si sólo es divisible entre el mismo y la unidad (1) 

Ejemplos:

• 1, 2, 3, 5, 7, 11, 13, 17 son números primos
• 3 es un número primo porque sus únicos divisores son 1 y 3.
• 7 es un número primo porque sus únicos divisores son 1 y 7.
• 4 no es primo porque es divisible entre 2; 12 tampoco lo es porque es divisible entre 2, entre 3, entre 4 y entre 6.

NÚMEROS COMPUESTOS 

Un número natural es un número compuesto si tiene otros divisores además de él mismo y la unidad (tiene tres o más). 

Ejemplos: 

4 es un número compuesto porque sus divisores son 1, 2 y 4. 

12 es un número compuesto porque sus divisores son 1, 2, 3, 4, 6 y 12.

CRITERIOS DE DIVISIBILIDAD

Son las características que reúne un número para asegurar que es divisible por otro, sin necesidad de efectuar la división.

Divisible entre 1

Todo número es divisible entre 1

Divisible entre 2

Un número es divisible por 2 si termina en 0 o en cifra par (2, 4, 6 y 8). 

Ejemplo: 

48 es divisible por 2 porque termina en 8 (cifra par) 

50 es divisible por 2 porque termina en 0.

Divisible por 3. 

Un número es divisible por 3 cuando la suma de sus cifras es múltiplo de 3. 

Ejemplos: 

42 es divisible por 3 porque la suma de sus cifras ( 4 + 2 = 6 ) es un múltiplo de 3.

Divisible entre 4

Si sus dos últimas cifras son 00 ó un múltiplo de 4 (12, 16, 20, 24, 28, 32, 36 y 40)

Ejemplos:

100 es divisible entre 4 porque termina en 00

4346 es divisible entre 4 porque termina en 36 que es múltiplo de 4 (4·9=36) 

Divisibilidad por 5. 

Si termina en 0 o en 5. 

Ejemplo: 

95 es divisible por 5 porque termina en 5. 

70 es divisible por 5 porque termina en 0.

Divisible entre 6

Si es divisible entre 2 y entre 3

Ejemplo:

126 es divisible entre 2 porque su última cifra es par y también es divisibles entre 3 porque la suma de sus cifras es múltiplo de 3:

1 + 2 + 6 = 9

Divisible entre 8

Si sus tres últimas cifras son 000 ó un múltiplo de 8 (104, 112, 120,...,992)

12000

7128

Divisible entre 9

Si la suma de sus cifras es un múltiplo de (9, 18, 27,...)

1269 es divisible entre 9 porque la suma de sus cifras es un múltiplo de 9

1 + 2 + 6 + 9 = 18

Divisible entre 10

Si termina en 0

10

20

100

6850

Divisible entre 11

Si la suma de las cifras que ocupan un lugar par menos la suma de las cifras de lugar impar es 0 ó múltiplo de 11 (11, 22, 33, 44,...)

3 9 2 7

la suma de las cifras en posiciones pares        9 + 7 = 16

la suma de las cifras en posiciones impares    3 + 2 = 5

la resta de ambos resultados                           16 - 5 = 11

11 es múltiplo de 11 por lo tanto 3927 es divisible entre 11

Divisible entre 12
Si es divisible entre 3 y entre 4

Divisible entre 13
Como 13 es un número primo, los únicos números divisibles entre 13 son los múltiplos de 13.

Divisible entre 14
Si es divisible entre 7 y entre 2

Divisible entre 15
Si es divisible entre 3 y entre 5

Divisible entre 25
Si termina en 00 ó en múltiplo de 25 (25, 50, 75)

Divisible entre 100
Si termina en 00